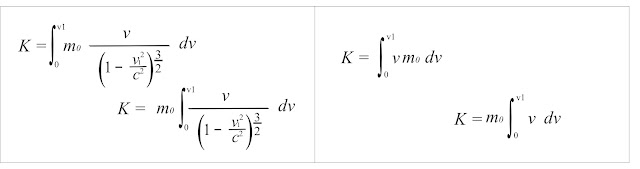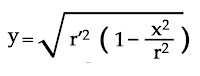Introducció:
Des de la teoria de la Transformació d'Hendrik Antoon Lorentz juntament amb la Teoria Especial de la Relativitat d'Albert Einstein, la física va canviar la manera i la naturalesa de percebre i veure l'univers.
Hendrik Antoon Lorentz, recolzant-se en el teorema de Pitàgoras, va deduir quina seria la relativitat de l'espai temps respecte a la velocitat passant a anomenar aquesta relació el Factor de Lorente, una relació que s'establiria per a un mateix fenomen físic entre dos observadors diferents amb diferent quantitat de moment o canvi i relacionat amb la velocitat de la Llum.
Lorentz tenia la convicció que la velocitat d'un objecte dependria de la velocitat de l'observador, i encara que Galileu feia referència a la mateixa qüestió afirmant que no hi havia diferència entre l'estat de repòs i el moviment, va ser Einstein qui va dir l'última paraula en afirmar que res no està en repòs absolut a l'univers i que s'hauria d'adaptar la Teoria de la relativitat assumint les conviccions de Lorentz, va ser llavors quan Albert Einstein va fer un èxit intel·lectual i va desenvolupar la Teoria Especial de la Relativitat.
El Experiment de Michelson y Morley: El Interferòmetre.
L'Experiment en si i sobre la base del seu plantejament va ser fallit. En poques paraules, va consistir a fer reflectir dos raigs de llum que recorrien una mateixa distància però per diferents trajectòries de manera que, tenint en compte el desplaçament de la terra, el recorregut d'un seria més gran al recorregut de l'altre i per tant el que afectaria a la interferència dels raigs reflectits en superposició.
Se'n va assumir la premissa que la velocitat de la llum és sempre la mateixa per a tots els observadors independentment del desplaçament de l'observador, és a dir, que si una persona viatja a la velocitat de la llum, aquesta seguiria veient la llum viatjar a 300.000 km/sg. D'altra banda, Albert Einstein va postular que la llum es corbaria per la influència de la gravetat en passar per les proximitats d'una estrella, és a dir, que estaria influenciada per G en la seva trajectòria, pel que al meu parer, el camp G de la Terra no deuria ser una excepció.
Penso que assumir que la velocitat de la llum és sempre la mateixa per a qualsevol observador a partir dels resultats de l'experiment no concloent de Michelson i Morley pot ser un error, de fet, trobo algunes incongruències que així m'ho indiquen, i en definitiva, de això va aquest article.
Esquema de l'experiment de Michelson y Morley:
Del fet que no es produís cap alteració, Lorentz es va plantejar que passaria si dos rellotges de llum exactament iguals i sincronitzats, tinguéssim un en repòs mentre que l'altre es desplacés per l'espai a velocitats properes a la Llum.
Esquema del suposat de Lorentz.
A partir d'aquí, va imaginar que el recorregut del raig de llum del rellotge que s'estaria desplaçant en (v) seria més gran que el del rellotge en estat de repòs, i recolzant-se a Pitàgores, va deduir quina seria la relativitat del temps entre els dos rellotges a partir de la comparativa entre la hipotenusa (recorregut de la llum en desplaçament) i la vertical (recorregut de la llum en repòs).
Ara ja podem comparar les equacions de relativitat de Galileu i Lorentz en direcció al movent a l'eix de x, sent y’ = y y z’ = z
Relativitat de Galileo
x’ = x – vt
Relativitat de Lorentz
x’ = g ( x – vt).
D'on es dedueix que el temps...
Abans de continuar, vull apuntar una conclusió que vaig extreure del principi de superposició, en el qual la Superposició seria el posicionament assolit dins un mateix pla espacial i temporal per un conjunt similar d'elements quan estan condicionats per la influència d'un límit comú que els caracteritza, cosa que fa que es mostren com una unitat des de la nostra perspectiva.
A l'anàlisi reflexiva que realitzo dins d'aquest blog sobre els diferents tipus de superposició, es pot comprovar com en el apartat dedicat a la síntesi additiva de llum, els camps a manca d'un límit, sempre se superposen, cosa que posa en evidència el càlcul realitzat en la Relativitat de Lorentz per obtenir la relativitat en desplaçament, una anàlisi matemàtica es van sumar erròniament els vectors de llum en comptes de superposar-los, tal com podem comprovar que passa a la natura. D'aquí neix tota la fantasia que fa més d'un segle que ens fa divagar amb els viatges temporals a través del univers.
Els deixo amb l'enllaç:
Principi de Superposició
LA TRANSFORMACIÓ DE LORENTZ.
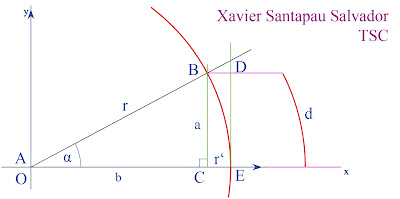
Experiment comparatiu dels dos rellotges de llum.
Si repassem el suposat comparatiu dels dos rellotges de Lorentz, podem veure com segons el principi de superposició, és impossible sumar al vector C el vector V horitzontal per límit trobat a C per a la superposició, de manera que la velocitat de la llum serà sempre la mateixa independentment del desplaçament horitzontal. Així, el primer error en l'experiment comparatiu dels dos rellotges de llum és intentar sumar dos vectors (C i V) quan clarament un es troba al límit.
El segon error és assumir que el raig de llum del rellotge en desplaçament no en té deriva i que traçarà la trajectòria diagonal sobre la hipotenusa. Està més que demostrat que tant un raig de llum com una ona electromagnètica trigarà 1,255 segons a assolir la Lluna, i que si apuntem a un punt concret de la mateixa, el desplaçament d'aquesta farà que el nostre raig de llum arribi a uns 1200 metres més enllà del nostre objectiu, cosa que demostra que la llum té deriva respecte al desplaçament de l'entorn, així que el raig del rellotge de Lorentz en moviment experimentarà una deriva progressiva en el desplaçament davant la impossibilitat de sumar ambdós vectors. La interpretació espacial de tal deriva la podem comparar a més amb la demostració de l'experiment de l'espira i el camp magnètic, on tant si mous l'imant com l'espira s'obté el mateix resultat, , tal i com va predir Maxwell qui va veure que estaven directament relacionat formant part de una mateixa cosa en tot el seu conjunt. Passarà el mateix si observes la trajectòria de la llum des de la Lluna i no des de l'espai i omets el teu desplaçament de l'equació.

Un altre error ho veurem més fàcilment amb el següent exemple.
La esfera de Llum de Albert i Henri.
Aquí i sota la premissa que la velocitat de la llum és la mateixa per a tothom a partir de les deduccions de l'experiment de Michelson i Morley, cadascun mesura la velocitat de la llum respecte així mateix com a centre d'una esfera lluminosa en expansió , i per tant, cadascú creu romandre al centre, i encara que el desplaçament de cadascun d'ells no afecti la velocitat de la llum, sí que ho fa en la seva posició respecte a l'origen, de manera que ells van perdent aquesta centralitat a favor del vector de desplaçament. Lorentz mantenia la tesi que cadascun romandria al centre de l'esfera lluminosa, però actualment, qualsevol astrònom pot corroborar l'evidència que Henri es desplaçaria sabent que tot el que observem al firmament forma sempre part del passat, és a dir, que les coses ja no són on les veiem.

Una manera de mesurar la velocitat real d'un objecte respecte a C podria estar en l'observació del desplaçament de les freqüències de llum que es deriven del desplaçament, ja que de la mateixa manera que la distància entre dos punts es pot mesurar pel desplaçament al vermell , l'acceleració respecte a un punt de llum es pot mesurar també mitjançant la comparació de la variació de totes les seves freqüències com a resultat del desplaçament a mesura que s'accelera.
Anem amb més exemples populars
Exemple de Henri Bergson a Brooklyn i el seu llançament de pilota.
D'aquest exemple se n'han fet moltes versions, des del tir a l'arc des d'un tren, encendre una llanterna, però prefereixo el clàssic per les casualitats, on Henri és capaç de llançar una pilota a la velocitat de 0.6C i també tenim Albert que es desplaça amb un vector velocitat de -0.6C a l'eix X de respecte a Henri.
Per simplificar l'exemple, acceptem que tant Henri com la Pilota tenen la mateixa massa, de manera que si Henri llança una pilota a 0.6C, aquesta sortirà contràriament a les observacions de l'exemple i segons la Tercera Llei de Newton a l'Espai a una velocitat de 0.3C, la diferència de velocitat entre Henry i Albert s'haurà reduït per tant a -0.3C. Des del punt de vista de la pilota, aquesta viatjarà respecte a Henry a una velocitat de 0,6C mentre que des del punt de vista d'Albert, la velocitat de la pilota és de 0.9C, un resultat casualment molt proper al 0.88C que es va obtenir en aplicar la Transformació de Lorentz.
Podem veure que els dos errors principals que no s'han contemplat a l'exemple de Henri Bergson a Brooklyn i el seu llançament de pilota són: l'aplicació de la Tercera Llei de Newton a l'espai i que la distància relativa de la llum a tenir en compte entre dos punts és de 2C.
Com veiem que l'exemple proposat, tal com es va plantejar, no ens resulta útil, faré alguns canvis per poder posar a prova la Tercera llei de Newton a l'espai i el principi de Superposició.
Suposem que l'Albert està ara en gairebé repòs absolut i que és Henri qui viatja per l'eix de la X a una velocitat de 0.6C. Tot i que aparentment és el mateix que el plantejament original, en la teoria de la relativitat clarament no és així si tenim en compte els límits a la propagació, la distància de 2C i lefecte de superposició.
Quan Henri llança la pilota en allò que es tracta sens dubte del millor llançament de la història, ho fa ara en el seu segon intent a una velocitat de 0.9C. Tenint en compte que el límit a la propagació de l'energia és C, aquest límit actuarà com un mur infranquejable per a totes les parts fent que la velocitat de la pilota respecte a Henri continuarà sent lògicament de 0.9C mentre que des del punt de vista de Albert qui roman absolutament immobilitzat pel majestuós llançament de Henri la velocitat de la pilota serà de 1C. i finalment, Henri viatgés ara respecte a Albert per l'eix de la X a una velocitat de 0.1C.
Els càlculs per al repartiment d'energia són els següents:
Velocitat d'Henri respecte a Albert: D0.6C
Velocitat de la Pilota D0.9C
respecte a Henri.
Apliquem la 3a Llei de Newton en superposició amb límit a C:
Per obtenir increment possible d'energia que pot absorbir la pilota respecte al límit C fixat per a la superposició serà el resultat de restar al límit C la velocitat dHenri.
[(1C
- 0.6C) =
0.4C]
La resta, la diferència entre l'energia absorbida per la pilota i l'energia inicial serà tota l'energia disponible per a Henri després d'aplicar la tercera llei de Newton en superposició
[(0.4C
- 0.9C) =
-0.5C ]
Pilota: +0.6C + 0.4C = 1C
Henri: +0.6C - 0.5C = 0.1C
Albert: 0.0C
De la 3ª Llei de Newton a l'Espai i el límit a la propagació de l'energia a C podem deduir que si per assolir una velocitat es necessita sempre el doble d'energia en un mateix espai de temps, una massa mai no podrà assolir la velocitat de la llum en ser sempre l'acceleració la meitat de la força aplicada i estar limitada en la propagació de la seva energia en C. Necessitaria doncs projectar més energia i més velocitat que la de la llum per poder assolir-la, per la qual cosa en la realitat i tornant a l'exemple del llançament de la bola d'Henri, està mai arribarà a assolir la velocitat de la llum per més que el càlcul ens demostri el contrari. Des del mateix punt de vista de la tercera llei de Newton, ha de passar el mateix per a les acceleració de partícules, estàs mai arribaran a assolir la velocitat de la llum per absorbir sempre la meitat de l'energia necessària per a tal velocitat.
Exemple de dos Coets i les boles de billar.
En aquest exemple, es planteja l'existència de dos coets que viatgen a la mateixa velocitat però en sentit contrari, i que tots dos deixaran anar una bola de billar perquè rebot amb la del seu contrari i retorni cadascuna al seu coet original. Al plantejament es fan diverses hipòtesis modificant l'estat d'un coet fins al punt de repòs absolut i atribuint tota l'energia al coet contrari, cosa que és pràcticament impossible.
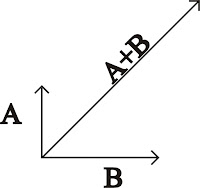
Albert Einstein realitza totes aquestes suposicions sense tenir en compte que el marc per a la comparativa relativa és de 2C i sabent que el límit a la propagació de l'energia per l'espai en C, raó per la qual no és possible la suma de dos o més vectors quan un s'hagi al límit. Així, l'obté els resultats relatius i interpreta que deformen la quantitat de massa en funció de la velocitat establint en g el factor de proporcionalitat entre la suma dels vectors A+B amb el vector A i en funció de B quan B = Velocitat de la llum, un fet que només és matemàticament possible.
Ometent la suma de vectors, com realitza en el supòsit d'un repòs absolut relatiu per a un dels dos coets, podem veure com els vectors d'alçada A i –A corresponents al moviment de la bola per a cada coet són sempre els mateixos independentment de la magnitud del vector B.
Lorentz & Einstein VS Galileo & Newton
El treball realitzat sobre un cos és igual a la integral de la força al llarg del camí pel qual el mou; aquest treball es converteix en energia cinètica.
Però la força modifica la quantitat de moviment…
I la quantitat de moviment depèn de la massa, que segons Einstein i a partir de Lorentz, també canvia amb la velocitat.
Però no des del punt de vista de Newton i Galileu.
L'energia cinètica es pot expressar com una integral de la velocitat que canvia des de l'estat de repòs fins que la força deixa d'actuar, tant per a Einstein com per a Newton.
Si la velocitat va de 0 a C.
Integrem entre 0 i v=C:
Fem l'anti-derivada però abans...
Hem de tenir en compte la tercera llei de Newton a l'espai, on es necessita el doble d'energia per vèncer la resistència al canvi, que és el mateix que multiplicar la velocitat per 2.
Suposem que mo·g és el valor de la massa m accelerada a velocitat C, suposició que fa que quadri amb el resultat esperat, doncs encara que no existís gamma, el resultat continuaria sent el mateix, però seguim amb el raonament.
a qualsevol velocitat, l'energia cinètica és igual a la variació de la massa per C al quadrat, com ja va deduir Newton,.
Com m0 és el valor de la massa en repòs, lenergia de la massa en repòs.
E0 será = m0 · c2
Sumant l'energia cinètica a l'energia de la massa en repòs, s'obté l'energia total del cos.
Conclusió:
Atesa la igualtat dels resultats i després de la comparativa entre els dos corrents, hauríem de tenir en consideració si l'èxit intel·lectual realitzat per Albert Einstein ha de romandre a la Física o limitar-se només a l'àmbit de les Matemàtiques, ja que si el seu punt de partida va ser assumir-les conclusions de Lorentz com a vàlides encara que actualment no se sustentin, arribant al mateix resultat que Isaac Newton sense la necessitat de corbar l'espai temps, potser no cal seguir mantenint a g en l'equació quan sense ella funciona exactament igual.
Finalment, també he de reconèixer que sense la Teoria Especial no ens haguéssim plantejat les noves teoritzacions que ens han fet arribar al marc de l'actual física de partícules.
 A
A