CÀLCUL DE LA DERIVA DE LA LLUM EN EL CAMP DE LA VIA LÀCTIA
Per calcular quina és la deriva que experimenta un raig de llum dins el camp de la Via Làctia quan es desplaça pel seu camp ens valdrem de la funció:
A partir d'ella, aïllarem la "y" per obtenir quina ha estat la deriva de la llum a l'alçada en què es troba l'observador.
Tenint present que "r' " és l'alçada del pont que descriu la trajectòria de la llum, serà aquesta dada juntament amb la velocitat de translació el que ens permetrà calcular la deriva per a la observació des de qualsevol punt del pla de la galàxia.
r' = ((r) x (Vat/C)) Diàmetre per Velocitat de translació i dividit per la Velocitat de la Llum.
DATOS:
Velocitat galàxia per el univers 555 Km/sg
Diàmetre: 190.000 anys llum.
Radi: r = 95.000 anys llum.
Gruix: 10.000 anys llum.
Període de rotació 225.000.000 anys.
Vat: Velocitat angular Translació en tot el seu radi exterior 220-240 Km/seg. (230 Km/seg de mitjana).
Hem de tenir present que la Via Làctica no és homogènia i que la velocitat de translació de la mateixa no és del tipus angular com passa en qualsevol moviment circular uniforme, sinó que es desplaça en bloc en una àmplia secció del seu radi, cosa que fa que la deriva tendeixi a ser més en diagonal que no pas circular dins aquest interval.
També hem de tenir present que totes les dades són aproximades ja que se'n desconeix la certesa exacta.

Si sabem que la distància del sol al centre galàctic és de 25.766 anys llum i coneixem els radis (r) i (r'), aplicant la fórmula podrem calcular que un raig de llum que hauria de passar pel centre de la circumferència i el sol experimentarà una deriva en alçada de x.
Anem cap la solució al càlcul de la alçada (r').
SOLUCIÓ AL CÀLCUL DE L'ALÇADA DE DERIVA EN CAMPS CIRCULARS
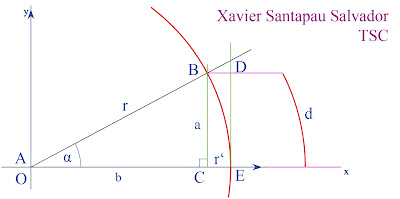
Per al càlcul de l'alçada aconseguida per la deriva de la llum al camp circulars com el de la Via Làctia ens valdrem de la funció sinus i del Teorema de Pitàgores.
Les dades que coneixem són:
r = 95.000 anys llum. (AB).
Pe Període = 240.000.000 anys.
Pr Perímetre = 2·π·r = 596902,60 a ll.
i busquem:
α : Angle del triangle.
a : Alçada del triangle rectangle (BC)
b : segon catet (OC)
r' : Alçada de deriva (CE)
Per poder calcular l'angle α haurem de conèixer d, que és el recorregut o el temps transcorregut durant el temps que triga la llum a recórrer la distància del radi. De qualsevol de les dues maneres obtindrem el mateix resultat.
En temps
d = t = 95.000 anys.
α = d · 360ᵒ / Pe = 95.000 · 360ᵒ / 240.000.000 = 0.1425ᵒ
En distancia
t = 95.000 anys.
d = Pr . t / Pe
d = 596.902,60 · 95.000 / 240.000.000 = 236,27394 a ll.
α = d · 360ᵒ / Pe = 236,27394 al · 360ᵒ / 596.902,60 = 0.1425ᵒ
Un cop tenim α calculem l'alçada a del rectangle a partir de la funció seno i el radi r.
sen (α) = a / r = BC / AB
a = sen(α) · r = sen(0.1425) · 95.000 = 236,2737039
i finalment només ens queda calcular b per completar tots els costats del triangle rectangle.
b = 94.999,706184 al.
Un cop coneixem b, m'adono que r' és l'ombra del recorregut corb sobre l'eix de la X, i que pel principi de proporcionalitat que he vist que existeix en cercles i anells en rotacio i que es dona entre els segments del seu arc definits pel desplaçament i la proyecció d'aquest sobre cada eix, sent alhora i a mode analògic estil Katherine, l'alçada de pont de deriva que busquem (r'). Aquest resultat ens servirà per obtenir l'alçada ens serveix per calcular la deriva que experimenta qualsevol vector en creuar una superfície circular en moviment uniforme mitjançant l'ús de la fórmula següent:
Ara ja podem calcular l'alçada de deriva restant b del radi r:
r' = r - b = 95.000 - 94.999,706184 = 0.293816 al.
Convertirem el resultat en anys llum a Kilòmetres...
0.293816 al · 9.460.730.472.580,8 Km = 2.779.713.984.531,8 Km.
i a partir de aquí, ja podem calcular l´alçada de deriva per a qualsevol punt de l´eix X de la galàxia.
Si la Terra està a X = 25.766 anys llum del centre, la alçada deriva en la seva posició serà de ...
y = 0,2828029 anys llum = 2.675.522.013.764,22072432 Km.
La deriva és de 2 Bilions de Km en el sistema europeu SIU .






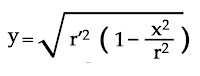


Cap comentari:
Publica un comentari a l'entrada