Perquè el número "e" se'n diu també Número Natural?

Introducció.

La raó del perquè al número "e" se'l coneix també com el nombre natural té el seu origen en la capacitat que posseeix aquest per representar certs fenomens donats a la natura. De la mateixa manera que la inversa del quadrat de la distància és una proporció que trobem tant en la força originada pels camps, o com de petita es fa una imatge a mesura que s'allunya de nosaltres, o com decreix el so a la distància,... i està relacionat amb tot allò que sigui lineal i que tingui a veure amb la distància, és a dir, entre dos punts, arribant a ser una proporció representada dins de nombrosos models físics i matemàtics, reflectint la realitat i per tant, considerada com natural, però en el número "e", on rau la seva naturalesa va més enllà de l'inversa del cuadrat de la distancia, així que seguim...

El nombre "e", que és un nombre irracional i conté infinits decimals, igual que la inversa del quadrat, també guarda una relació directa amb allò natural, i entendre quina és aquesta relació és del que pretén tractar el següent article, per això que per intentar mostrar-la, he de recórrer els passos que van permetre la seva troballa i deixar així de forma més clara la relació que li permet ser el nombre natural, ja que lamentablement, tinc la sensació que molts dels nombrosos articles publicats sobre ell suspenen a l'hora d'establir i clarificar aquesta relació. Espero no defraudar-los.

Per això, no m'estendré en demostracions, sobretot quan a Internet n'està ple, sinó que intentaré només esmentar els mètodes seguits per Leonhard Paul Euler, important: catedràtic en Filosofia Natural i fidel seguidor de la física de Newtons des de l'òptica de les matemàtiques", i arribar a relacionar allò natural amb la constant "e".

Origen.

El seu origen ve del famós problema de l'interès que va ser plantejat per Jacob Bernoulli, encara que ja amb anterioritat, Jonh Napier, havia estat treballant amb ell a les seves taules logarítmiques sense arribar a concretar-ho. Finalment, va ser Leonhard Euler qui li va saber veure tot el potencial, extreure'l de l'aritmètica i aplicar-lo a la geometria. Però no avancem esdeveniments i anem pas per pas, així que comencem per veure en que consisteix el problema aritmètic de l'interès.

És tracta d'un problema on es planteja com s'incrementa el benefici obtingut en un préstec a un any i com l'interès acumulat decreix a mesura que es divideix el temps en intervals cada vegada més petits a l'hora de comptabilitzar l'interès i treure'n el màxim benefici. El problema parteix del període global i inamovible de 1 any. Quan solucionem el problema podem veure com a mesura que s'incrementen els intervals, el creixement del benefici obtingut en aplicar l'interès va disminuint gradualment en el que és una sèrie convergent, i finalment, el capital més el interés acumulat en dividir el periode en infinitat de intervals, troba un sostre que és: "e = 2,71828182845904523536028747..." és a dir, que "e" es converteix en el límit de la funció quan n tendeix a infinit.

Per mi, el que més importa d'aquest exemple no és el que es ressalta a la majoria d'explicacions amb l'existència d'un límit aritmètic en tractar-se d'una sèrie convergent, que és molt important, sinó que el més important per mi és que hem representat un creixement constant i continuat d'alguna cosa, en aquest cas del capital, durant tot l'interval de temps que dura l'any, és a dir, un creixement de manera continuada i ininterrompuda, tal com passa a la natura, i que aquest creixement exponencial ve limitat en un valor "e".

Vegem un breu resum dels passos seguits per trobar la solució del problema:

Primer es calcula un interès anual del 100% a 1 any (1+1) per poder comparar amb altres supòsits.

1 + 100% de 1 = 2

En el segon cas, dividim l'any en dos períodes i apliquem el mateix interès però ara de manera semestral, així l'interès aplicat al segon semestre és sobre la suma del capital més l'interès generat durant el primer semestre (1+ 1 /2)., sent el resultat 2,25.

La següent vegada, ho fem per quadrimestres dividint el període en tres intervals i tornem a fer el mateix càlcul: 2,37.

I així successivament fins a arribar a dividir l'any en infinits intervals, i veient com el creixement del capital va disminuint a mesura que afegim intervals, fins a trobar que la suma total de la sèrie infinita ens dóna el número “e”.

∑ (1 + 1/n)n

sent "e" el límit de la mateixa entre n=0 i l'infinit.

i que també es pot representar mitjançant factorials com:

i gràficament on "e" és l'asímptota vertical de la funció.

Altres de les sèries més populars estudiades per Euler per la seva relació amb el nombre pi, i que al meu parer, formen part del camí recorregut per establir la naturalesa del nombre "e" van ser:

La suma dels inversos dels nombres naturals elevats a n:

∑ (1 + 1/2^n) = 2

La suma dels inversos dels quadrats dels nombres parells:

La suma dels inversos dels quadrats dels nombres imparells:

La suma de tots els inversos dels quadrats:

∑(1 + 1/n^2) = 1,6449 = (Pi^2)/6

Vull ressaltar una de les sèries que en alguns àmbits és atribuïda a Euler de manera errònia, i és la divisió dels productes dels nombres naturals parells entre els imparells, o dit també el quadrat dels nombres parells entre el quadrat dels nombres imparells :

Aquesta en realitat va ser trobada per Johannis Wallis, fundador de la Royal Society, qui havia trobat aquesta fórmula per trobar el número Pi representant-la com:

Curiosament, poden veure que en aquesta fórmula també podem trobar rastres de la proporció universal del quadrat de la distància representada en quadrats numèrics tant al numerador (parells) com al denominador (imparells), així que d'alguna forma, aquesta proporció "1 /x^2" i la seva inversa "x^2" amaguen una relació entre l'aritmètica i la geometria, i és aquesta relació la que per a mi, Euler va saber trobar, comprendre i expandir amb "e" a l'univers del coneixement.

*Anotacions d'Euler:

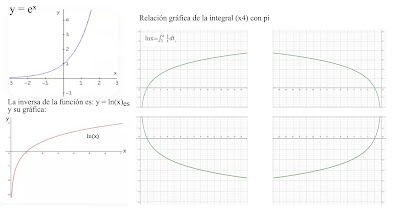
Així, d'alguna manera, totes les sèries convergents estan relacionades amb el número pi en tractar-se d'una corva que tendeix des d'un punt definit cap a un altre, cosa que podem intuir clarament quan col·loquem i sumem quatre àrees d'una mateixa funció convergent a mesura que girem el pla 90 graus, obtenint una imatge que tendeix en general a ser ovalada, és a dir, que l'àrea de la funció corva convergent guardarà una relació directa amb el número pi^2.

Per mostrar-vos-ho,  he agafat una mateixa gràfica d'una funció convergent i l'he anat girant en un tallar i enganxa de 90 graus per mostrar com la imatge resultant s'assembla a una el·lipse.

El següent pas fet per Euler en la cerca de trobar la constant natural e-exponencial va ser trobar la funció exponencial on la seva derivada fos si mateixa. Posant-me al seu lloc, tot em fa pensar que la idea li va sorgir de l'estudi de les sèries convergents i divergents, trobant i classificant quins eren convergents i quins divergents fins a comprendre com en funció de la base, una mateixa sèrie podria ser convergent i divergent, es a dir, constant, que per la qual cosa es va haver de plantejar quin seria el nombre a partir del qual aquesta convergència i divergència fossin la mateixa cosa, és a dir, trobar el número on una sèrie exponencial deixaria de ser convergent i passaria a ser divergent i viceversa. 

A la següent imatge dels meus apunts, recullo la progressió que va fer Euler per trobar la funció que fos igual a la seva derivada, de manera que el seu creixement fos continuat i en totes direccions en ser el ritme de canvi la pròpia funció. Com he esmentat amb anterioritat, hi ha múltiples vídeos i documents a Internet que expliquen tot el procés, per la qual cosa no l'he exposat més aquí. El més important per a mi és que entenguin com a Euler, mitjançant la recerca de la constant que fes que la funció exponencial fos igual a la derivada, es va adonar que estava representant aritmèticament una de les lleis més importants de l'univers, la conservació del moment, moviment, energia, .... i és que la fórmula d'Euler pot representar fidelment tant la manera que té l'energia de propagar-se sempre a velocitat constant i en totes direccions disminuint-ne només la quantitat, com qualsevol altre fenomen donat a la naturalesa que tingui un creixement exponencial constant i continuat, com per exemple la vida en la seva renovació cel·lular, el creixement demogràfic,... encara que en aquests casos i a diferència de la propagació de l'energia, la quantitat del moment es renova a cada moment conservant-se íntegrament en el seu origen en donar-se una substitució, i és per això precisament i per les seves moltes coincidències amb fenomens naturals que, el número “e”, ha adquirit el sobrenom de Nombre Natural dins de les matemàtiques. 

Així, el número "e" ens està representant la propagació exponencial a ritme constant de qualsevol cosa en el temps gràcies al límit que suposa el mateix número "e" per a la funció exponencial, podent aplicar-se per modelar l'expansió en totes direccions, tal i com passa en nombrosos fenòmens naturals. Aquesta característica fa que la funció també pugui representar ones mitjançant la participació dels nombres complexos, transformacions com el creixement demogràfic, la dissipació de l'energia, el temps, la superposició de camps, de energía o qualsevol altre tipus de superposició que necessiti d'un límit,... en definitiva, qualsevol cosa que s'expandeixi a l'univers de manera continuada, en totes direccions, a velocitat constant i resultat accelerat, guardant així una relació directa amb la naturalesa física més expansiva de l'univers, fins i tot el propi Univers, s'expanderia en totes direccions creixent exponencialment el seu espai en base a "e".

Més tard, i amb l'aplicació dels nombres complexos, les seves conclusions l'elevarien a la posició que s'ha guanyat justificadament dins dels grans Mestres de la Física i la Matemàtica, però aquesta qüestió més complexa i cíclica suposaria escriure un altre article, i crec que ho van trobar i entendre de sobres en qualsevol portal com la Wikipedia.

També pretenia en un principi parlar-los de l'estudi de les sèries infinites que permeten assolir més ràpidament el nombre pi realitzat per part de Rāmānuja Āchārya, que pujant a una escala de manera molt més que intel·ligent, amplica d'una manera sorprenent creant eines i estratègies que han resultat molt útils per a la computació gràcies a l'estalvi de temps i recursos que suposa la seva aplicació, relacions que a causa de la meva incapacitat per relacionar-les, les percebo més com a complexes eines que sincerament, no aconsegueixo comprendre ben bé com funcionen, sense que per això no les deixi d'admirar.

Els deixo algunes, per si es volen entretenir-se en la recerca.

Nota final.

Espero haver-los donat una explicació prou comprensible de l'origen del nombre "e" i del que representa aquest en tots els diferents mons del coneixement: geometria, aritmètica, física, química, banca, ...  doncs ho he fet tan bé com he pogut. Aprofito per mencionar que aquest projecte forma part de un grup de treballs que he anat realitzant en diferents blocs sobre camps G i M, intel·ligència natural, superposició,... dels quals poden trobar enllaços directes dins del meu perfil, i espero que no hagin resultat del tot una pèrdua de temps i acabin per trobar cadascun la seva utilitat, així que sense res més a dir, em retiro sense anar-me'n, una mica cansat de pensar somiant sense obtenir més que la meva pròpia satisfacció a canvi, que és el que em passa sempre i que sospito que és degut al fet de no tenir cap títol que pugui avalar la meva trajectòria ni em permeti formar part de cap comunitat, excepte de la generalitzada humanitat i la seva cultura popular, i aquí estic.

Finalment, mil gràcies a tota la gent que comparteix coneixement lliurement, ja que són ells els que m'han proporcionat la senda que m'ha permès passejar pel fascinant camí de la ciència.