La visió complerta d'aquesta demostració la podeu llegir a l'apartat dedicat a l'anàlisi del CAMP ESTÀTIC clàssic del meu treball on queda clar que és la superposició dels camps per alineament d'espín i trajectòria la responsable de l'amplificació dels camps, i el desplaçament dels electrons és una qüestió secundària que només influeix en el posicionament que adopten els electrons en canviar el camp mitjà mitjançant una diferència de potencial i fer aquest desplaçament.
https://teoriaespacialdecamps.blogspot.com/2023/04/camp-unificat-unified-field.html
Una de les raons que per mi ha incentivat la idea de la física quàntica ha estat la dificultat de comprendre quin camp i partícula són parts d'una mateixa cosa, que tots dos es desplacen per igual en la component del seu vector desplaçament, tal com valora la física clàssica, i que el camp posseeix alhora un vector angular afegit que és el responsable de la força i per tant, de la resistència al canvi. És aquí on entra en escena la fórmula d'Euler, capaç de representar tots dos vectors recolzant-se en la periodicitat cíclica que proporcionen l'aplicació dels nombres complexos, va resultar ideal per representar aquesta rotació i translació simultània.
Una altra de les raons que considero que han incentivat la imaginació científica per a la nova física ha estat per mi la dificultat per diferenciar el camp particular del camp de forces. Mentre que camp particular i partícula es desplacen linealment, és el vector angular del camp particular el principal responsable de la resistència al canvi en comportar-se aquest com un perfecte giroscopi, i que combinat amb la component del vector desplaçament (lineal), formen en conjunt el que reconeixem com els responsables del camp de força/resistència. Per diferenciar-los, quan el vector camp és principalment angular parlarem de camps polaritzats determinant-ne el signe per la regla de la mà dreta, mentre que quan parlem del vector de desplaçament estarem dins del marc lineal del concepte clàssic d'inèrcia.
Un tercer aspecte a tenir en compte és que mentre que la resistència o força del camp del vector desplaçament és lineal, al vector angular és global i està directament relacionat amb la velocitat angular, és a dir, la força/resistència angular que exerceix el camp en rotació a una mateixa distància radial és igual en tot el seu perímetre angular respecte a l'eix, cosa que fa que es conservi en tot moment la quantitat total d'energia angular produint-se en resposta a la interacció un canvi de la posició espacial de la partícula lligada al camp, i per tant, un canvi en el seu vector de desplaçament que passa de ser lineal a traçar una corba (El comportament és similar a la curvatura que experimenta qualsevol pilota quan la copegem amb efecte, la resistència al canvi que produeix l'espín fa que aquesta viri en la seva trajectòria traçant una corba a l'espai, de la mateixa manera que ho faria qualsevol partícula o massa amb espín propi que experimenta una interacció en el seu camp angular).
Tornant a caràcter global del camp particular en espín, penso que és molt probable que també sigui la responsable que puguem observar efectes de simultaneïtat que ens semblen escapar alhora quan observem dos punts distants del camp d'una mateixa partícula o grup de partícules.

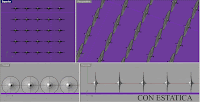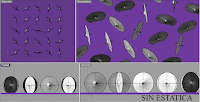
Per distingir millor la imatge d'ona respecte a l'espín de la partícula, seguint molts exemples de la xarxa, he alentit el temps a t/3, estirant així l'ona per a una millor observació.
A les imatges, la partícula B té el seu espí invertit respecte a la partícula A i la partícula C té el seu espí amb doble velocitat angular respecte a la mateixa partícula A.
A les següents imatges, es mostra el camp des de la perspectiva de Schrödinger i seguit la mateixa representació de les tres partícules però amb el temps sense alentir.
Així, penso que mitjançant l'aplicació de l'Equació de Schrödinger per intentar predeterminar la incertesa que provoca la nostra intrusió i el camp mitjà per a la detecció d'una partícula a partir de la seva ona, apareixen noves eines com la Transformada de Fourier que permet calcular la seva intrusió velocitat, donant origen a altres eines que construiran pas a pas la nova física quàntica: la física de les ones.












Cap comentari:
Publica un comentari a l'entrada